Due approcci alla probabilità
In qualsiasi analisi di dati, la statistica è uno strumento chiave. Due approcci fondamentali della statistica, frequentista e bayesiano, vengono comunemente utilizzati in vari settori della scienza e della tecnologia. Questi due metodi offrono due modi diversi di capire e interpretare la probabilità, perciò comprendere la differenza tra questi approcci è essenziale per prendere decisioni informate.
Approccio Frequentista
La statistica frequentista è l’approccio tradizionale alla statistica. Si basa sull’idea che le probabilità sono relative alla frequenza di un evento in un lungo numero di ripetizioni. Un parametro (una quantità sconosciuta che caratterizza una popolazione) è considerato fisso e l’incertezza è determinata dalle variazioni negli esiti dei dati.
I frequentisti utilizzano metodi standardizzati per testare le ipotesi e calcolare gli intervalli di confidenza. Questi metodi si basano sull’idea che i dati sono un campione casuale della popolazione e che le caratteristiche della popolazione (come la media e la varianza) possono essere stimate a partire dal campione. Inoltre, esaminano i dati da un punto di vista oggettivo, senza considerare precedenti conoscenze o convinzioni.
Approccio Bayesiano
La statistica bayesiana prende il nome dal matematico britannico Thomas Bayes e offre un approccio alternativo alla statistica. A differenza dei frequentisti, i bayesiani interpretano la probabilità come una misura soggettiva. L’analisi bayesiana permette infatti di incorporare le proprie convinzioni sul valore di un parametro sconosciuto, utilizzando una distribuzione di probabilità. Pertanto, è possibile assegnare una probabilità a un’ipotesi o a un parametro specifico. L’arrivo di nuovi dati permette poi di aggiornare queste convinzioni.
Prima di avere a disposizione qualsiasi informazione, le convinzioni soggettive sono descritte attraverso una distribuzione di probabilità chiamata distribuzione a priori. Dopo aver raccolto e analizzato i dati, le convinzioni sono aggiornate e rappresentate dalla distribuzione a posteriori.
La statistica bayesiana utilizza il Teorema di Bayes per aggiornare le probabilità, quindi per passare dalla distribuzione a priori alla distribuzione a posteriori. Il teorema afferma che, dati due eventi A e B, la probabilità post-osservazione (o a posteriori) di un evento 
, alla luce dell’arrivo di nuovi dati, è proporzionale alla probabilità pre-osservazione (o a priori) di quell’evento 
moltiplicata per la probabilità di osservare i nuovi dati, dato l’evento 
.
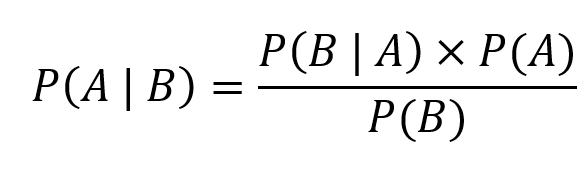
Esempio Pratico
Immagina di voler sapere se una moneta è equilibrata.
Un frequentista lancerà la moneta molte volte, contando quante volte esce testa e quante volte esce croce. Supponiamo che su 100 lanci, la moneta mostri 60 volte testa. Questo è espresso come:
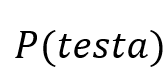: probabilità che il risultato del lancio della moneta sia testa. Se questa probabilità è uguale al 50%, la moneta è equilibrata.
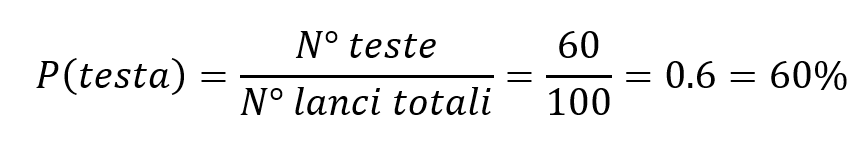
Da questi dati, il frequentista dedurrà quindi che la probabilità di ottenere testa al lancio di una moneta è del 60%.
Un bayesiano, al contrario, inizia con una credenza preliminare sulla probabilità che la moneta sia equilibrata; questa credenza, nota come a priori, potrebbe essere basata su esperienze precedenti con altre monete. Successivamente, lancerà la moneta molte volte e aggiornerà la sua credenza iniziale sulla base dei risultati. Se ottiene 60 volte testa su 100 lanci, la probabilità aggiornata, o post-osservazione, che la moneta sia equilibrata sarà diversa da quella precedente all’osservazione. Questo è espresso come:
- A : l’evento basato sulla convinzione iniziale che la moneta sia equilibrata.
- B : l’evento osservato.
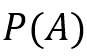- : probabilità pre-osservazione (a priori), fondata sulla convinzione iniziale (50%).
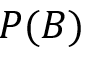: probabilità post-osservazione (a posteriori), relativa alla frequenza (60%).
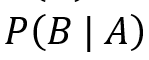: probabilità di ottenere il risultato osservato, data la probabilità a priori (50%).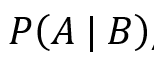- : probabilità aggiornata che la moneta sia equilibrata, data la probabilità a posteriori.
La formula di Bayes sarà quindi:
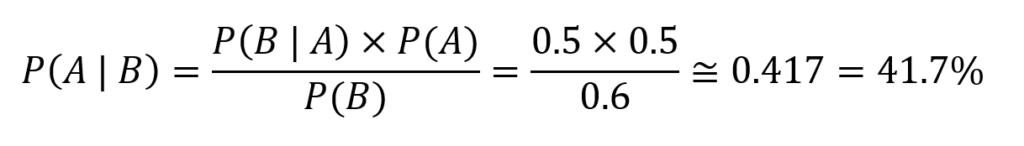
Secondo l’approccio bayesiano, la probabilità che la moneta sia equilibrata, dopo aver osservato i risultati dei lanci, è quindi del 41.7%.
Conclusione
Entrambi gli approcci alla statistica hanno i loro punti di forza e di debolezza. La statistica frequentista è utile per le sue tecniche standardizzate e per l’interpretazione oggettiva delle probabilità. La statistica bayesiana, d’altra parte, è utile per il suo approccio flessibile e per la sua capacità di incorporare informazioni priori. La scelta tra questi due approcci dipenderà dal contesto specifico e dalle esigenze del ricercatore.
Articolo scritto in collaborazione con Maria Sole Chiaramonti