Distribuzioni disaggregate:
Presa in considerazione una distribuzione disaggregata ordinata in senso crescente 
, il valore centrale è la media aritmetica dei termini estremi:
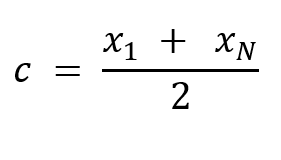
Esempio:
Supponiamo di voler determinare la temperatura media di una città in un determinato giorno. Le temperature rilevate nel corso della giornata sono: 20°C, 22°C, 18°C, 24°C, 21°C, 19°C, 23°C.
Ordiniamo i dati in modo da individuare chiaramente l’estremo inferiore e quello superiore:
18°C, 19°C, 20°C, 21°C, 22°C, 23°C, 24°C.
Calcoliamo il valore centrale:
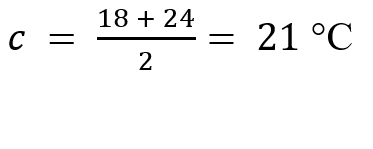
Quali proprietà ha il valore centrale?
Una peculiarità del valore centrale è che coincide con la media aritmetica se i valori ordinati della distribuzione sono tutti diversi ed equidistanti, ovvero tali che la differenza tra un valore e il precedente sia costante.
Proviamo a verificare se questa proprietà vale anche nel nostro esempio:
Calcoliamo la media aritmetica dei dati sulla temperatura a nostra disposizione, i quali presentano i requisiti necessari, ovvero di eterogeneità ed equidistanza:
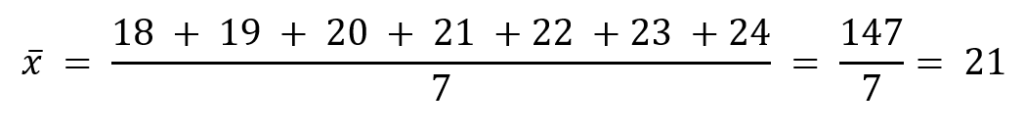
Otteniamo che la temperatura media in città quel giorno è di 21°C, che corrisponde al valore centrale, quindi la proprietà è valida.
Articolo scritto in collaborazione con Marta Iacolino