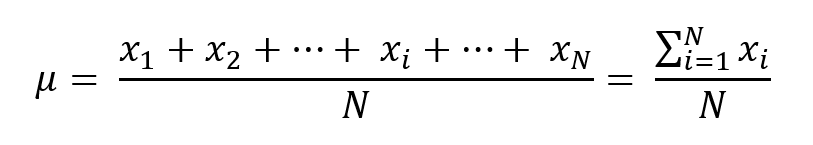Tag: statistica descrittiva

MEDIANA

Cosa è la mediana?

La mediana, che indicheremo con il simbolo, è un indice di posizione delle medie lasche che rappresenta il valore centrale di una successione ordinata, in senso crescente o decrescente, di valori. In altre parole, è il valore tale per cui prima e dopo ci siano il 50% delle osservazioni.

Quando la si utilizza?

La mediana, a differenza della media o altri indici di posizione analitiche, può essere utilizzata sia per variabili qualitative ordinabili sia per variabili quantitative, mentre non può essere calcolata per variabili qualitative sconnesse. Inoltre, non si distorce in presenza di outlier a differenza degli indici di posizione analitiche (medie).

Leggi tutto “MEDIANA”

MEDIA QUADRATICA

Perché è utile?

La media quadratica fornisce una misura della dispersione dei dati rispetto alla media aritmetica. In particolare, essa indica quanto la deviazione dei singoli dati dalla media aritmetica è influenzata dalla loro grandezza. In altre parole, valori molto grandi o molto piccoli, essendo elevati al quadrato, avranno un’incidenza maggiore nella media quadratica rispetto ai valori intermedi. Questo la rende particolarmente utile in ambiti come la fisica o l’ingegneria, dove spesso si lavora con dati che possono assumere valori sia positivi che negativi. La media analitica di ordine 2 corrisponde alla media quadratica.

Leggi tutto “MEDIA QUADRATICA”

MEDIA ARMONICA

Cos’è e quando è necessario utilizzarla?

La media armonica di una successione di valori  tutti diversi da 0. Corrisponde alla media analitica di ordine p = -1. La si utilizza quando si necessita di una media che ripartisca l’intensità globale del fenomeno, rispetto al tempo, allo spazio e così via. Ad esempio, viene spesso usata quando si ha a che fare con dei rapporti, per studiare grandezze inversamente proporzionali come tempo e velocità o prezzo di un bene e potere d’acquisto di una moneta.

Leggi tutto “MEDIA ARMONICA”

MEDIA ARITMETICA

Com’è definita?

La media aritmetica è certamente quella più nota e utilizzata nella statistica. È la media analitica di ordine p = 1 e potremmo definirla come il valor medio di una successione di valori .

Come si calcola?

Calcolare la media aritmetica, solitamente indicata con μ o  , equivale a sommare tutti i valori della distribuzione (xi)  e poi dividerli per la numerosità del campione N:

Leggi tutto “MEDIA ARITMETICA”

Indici di posizione (medie)

Perché abbiamo bisogno di calcolare le medie? A cosa servono?

Le medie consentono di sintetizzare in un solo valore rappresentativo l’intera distribuzione di dati.

Esempio:

Ad esempio, se volessimo avere un’idea di quanto guadagnano gli impiegati di un’azienda con 20mila addetti, invece di riportare i singoli stipendi è molto più comodo ed efficace calcolarne la media, in modo da ottenere un unico valore che sintetizza lo stipendio di un addetto.

Le medie possono essere di due tipi:

  • Analitiche
  • Lasche

Leggi tutto “Indici di posizione (medie)”

3 passi fondamentali per la preparazione dei dati

Chi ben comincia è già a metà dell’opera

Se hai raccolto i tuoi dati ricordati che la qualità dei dati è importantissima per la tua analisi.

Prima di eseguire qualsiasi test o modello è necessario:

  1.  Effettuare le statistiche descrittive
  2.  Controllare gli outlier
  3.  Comprendere dalle statistiche descrittive se vi sono problemi, come ad esempio degli NA (dati mancanti).

Se tutti questi 3 passi sono stati eseguiti correttamente, avrai dei dati che, statisticamente parlando, sono buoni per la analisi e avrai un idea, grazie alle statistiche descrittive, di come sia composto il tuo campione. Da ciò potrai formulare ipotesi da testare con i modelli o test.

Leggi tutto “3 passi fondamentali per la preparazione dei dati”

Frequenze: cosa sono e quali sono?

Frequenze, indici indispensabili per comprendere i tuoi dati qualitativi

  • La frequenza assoluta è il numero o conteggio delle unità che rientra in una determinata classe (intervallo) o fattore.
  • La frequenza relativa è la frazione o la percentuale di unità, rispetto al numero totale di unità, che ricade in una determinata classe (intervallo) o fattore. La somma di tutte le frequenze relative è 1 o in caso percentuale, 100%.
  • La frequenza cumulata è la frazione o la percentuale di unità che è inferiore ad una data soglia. La prima soglia sarà  uguale alla soglia della frequenza relativa, la seconda soglia sarà la somma della prima e della seconda soglia di frequenze relative e così via. L’ultima soglia sarà la somma di tutte le frequenze relative.

Leggi tutto “Frequenze: cosa sono e quali sono?”