Come comprendere se un modello è valido
R2
Il coefficiente di determinazione (R quadro) è un indice che misura il legame tra la variabilità dei dati e la correttezza del modello statistico utilizzato. Esso è legato alla frazione della varianza non spiegata dal modello. Tale indice varia da 0 a 1, più si avvicina ad 1 più il modello riesce a spiegare i dati. Tale indice è solitamente utilizzato nei modelli di regressione lineare. R2 tende a sovrastimare la bontà del modello nel caso in cui il modello sia in overfitting, ovvero quando il modello ha troppe variabili X. Per correggere tale problematica solitamente si fa riferimento ad una correzione di tale indice chiamato “R2 corretto” che penalizza i modelli eccessivamente complessi.
Esempio:
Il seguente esempio analizza la relazione, tramite un modello lineare, tra peso e altezza.
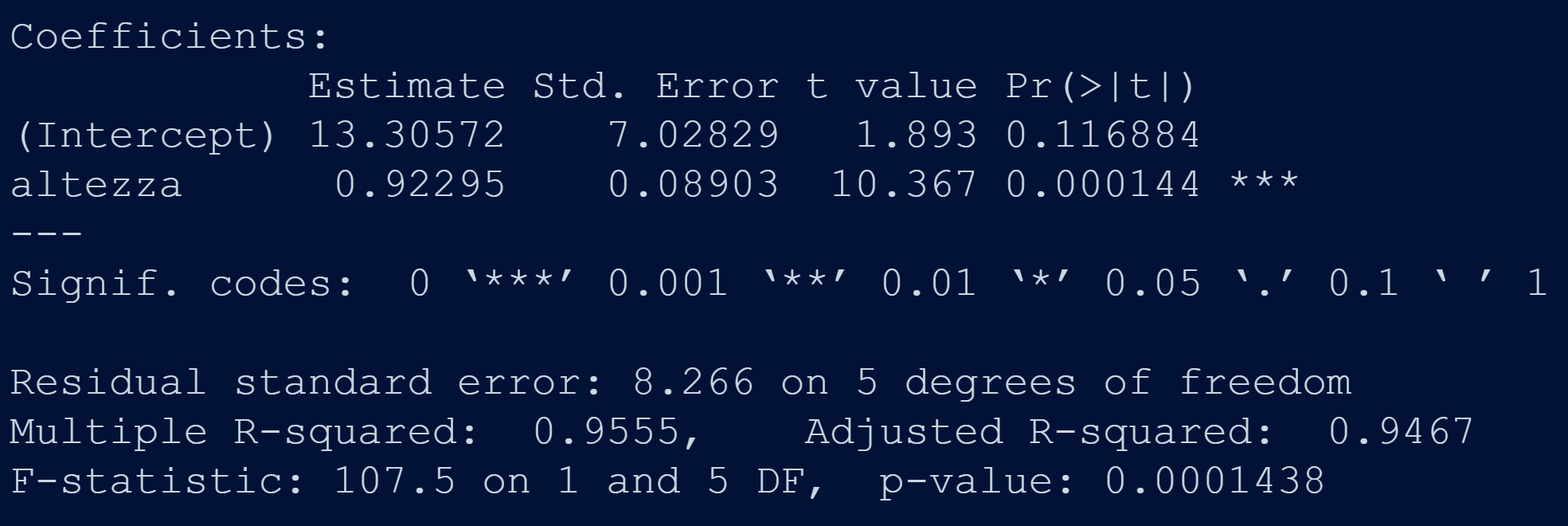
Dal coefficiente di determinazione (R quadro) osserviamo come il modello si adatti correttamente ai dati. L’altezza può essere spiegata al 95,55% dal peso.
Pseudo R2
Tale indice rappresenta una sottostima del R2, viene utilizzato quando non è possibile calcolare R2. Anch’esso ha una versione corretta che penalizza i modelli eccessivamente complessi. Solitamente viene calcolato nei modelli logit e probit o nelle loro trasformazioni (multinomial, conditional, mixed, ecc.).
AIC
Il criterio d’informazione di Akaike, è un metodo per la valutazione e il confronto tra modelli statistici. Fornisce una misura della qualità della stima di un modello statistico tenendo conto sia della bontà di adattamento che della complessità del modello. È basato sul concetto di entropia come misura di informazione, tramite cui valuta la quantità di informazione persa quando un dato modello è usato per descrivere la realtà. La regola è quella di preferire i modelli con l’AIC più basso. È un criterio di valutazione molto utile perché permette di confrontare tra loro anche modelli non annidati.
BIC
Il criterio è simile all’AIC ed è utilizzato per la valutazione e il confronto tra modelli, ma a differenza dell’AIC penalizza maggiormente i modelli eccessivamente complessi.