Indice di correlazione di Pearson

Indicatore della relazione lineare

È un indicatore che misura la relazione lineare, in termini di forza e direzione, tra due caratteri quantitativi X e Y. Si dice che tra X e Y vi è correlazione positiva o concordanza se crescono o decrescono contemporaneamente. Si ha correlazione negativa o discordanza quando al crescere di un carattere, l’altro tende a decrescere.

Come si calcola?

L’indice di correlazione lineare di Bravais-Pearson è dato dal rapporto tra la codevianza di X e Y e il prodotto delle deviazioni standard dei due caratteri:

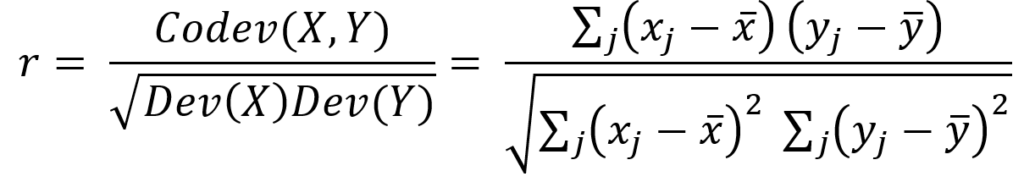
Proprietà:

è un numero puro, adimensionale: privo di unità di misura
varia nell’intervallo [-1,1]; i valori estremi -1 e 1 si hanno se e solo se tra le variabili X e Y c’è perfetta relazione lineare; in particolare, è pari a -1 quando tutti i punti (x_i, y_i) sono perfettamente disposti su una retta con coefficiente angolare negativo, mentre è uguale a 1 quando tali punti sono allineati su una retta con coefficiente angolare positivo.
È invariante rispetto a trasformazioni lineari: non cambia se le modalità della singola variabile vengono moltiplicate oppure aumentate o diminuite di una costante positiva.
È simmetrico ovvero non varia al variare del ruolo di X e Y:

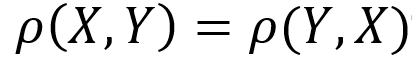
Interpretazione

Se il valore dell’indice di correlazione è pari a:

+1: c’è perfetta correlazione lineare positiva tra i due caratteri, all’aumentare di uno aumenta anche l’altro in modo lineare o direttamente proporzionale
-1: c’è perfetta correlazione lineare positiva tra i due caratteri, al diminuire di uno diminuisce anche l’altro in modo lineare o direttamente proporzionale
0: al crescere di X, Y non varia quindi non c’è alcuna relazione lineare tra X e Y; potrebbe tuttavia esserci una relazione non lineare.

Regole per poterlo utilizzare:

Bisogna effettuare dei controlli preliminari sulla distribuzione e sul tipo di relazione tra i due caratteri e verificare la presenza di valori anomali, prima di poter procedere con il calcolo dell’indice; in particolare, è indispensabile accertarsi che:

I due caratteri siano entrambi quantitativi, ovvero assumano valori appartenenti all’insieme dei numeri reali
I due caratteri abbiano entrambi una distribuzione normale, ovvero la loro funzione di ripartizione deve essere tale che:

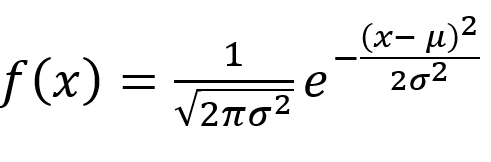
Non siano presenti outliers (valori anomali) ed eventualmente bisogna rimuoverli
La relazione tra i due caratteri sia di tipo lineare, e non quadratica o di altro tipo.

Articolo scritto in collaborazione con Marta Iacolino