Analizzare e comprendere i dati
La statistica descrittiva è composta da vari indici usati per descrivere e sintetizzare le caratteristiche di base dei dati raccolti. Insieme alla semplice analisi grafica, la statistica descrittiva costituisce la base di partenza di qualsiasi analisi.
Perché ci è utile la statistica descrittiva?
La statistica descrittiva fornisce una sintesi semplice del campione, aiuta a comprendere se ci sono errori nei dati raccolti e ci fornisce le basi per formulare le ipotesi.
Perché non basta la statistica descrittiva per spiegare tutto?
La statistica descrittiva si limita a rappresentare l’informazione contenuta nei dati raccolti, ma occorre la statistica inferenziale per comprendere il perché delle differenze rilevate nella statistica descrittiva.
Quali sono gli indici che posso usare per la statistica descrittiva ?
A seconda della natura delle variabili (colonne) nel dataset occorrono differenti statistiche descrittive:
Se hai dei dati quantitativi (continui) potrai usare molti indici come:
Indici di posizione: i più famosi sono media, moda, mediana.
Indici di variabilità: il più utilizzato è la varianza.
Se hai dati qualitativi (fattoriali, dummy, ecc…) potrai usare alcuni indici come le frequenze.
La scelta degli indici dipende dalla natura dei dati, nel seguente esempio ne vedremo alcuni:
Esempio 1: Genere
Il seguente dataset riguarda il disastro del Titanic. Cercheremo di comprendere le informazioni che possiamo estrapolare con facilità dai dati senza dover fare ipotesi. Quanti uomini e donne erano sulla nave?
| Genere | N | Frequenza relativa | Frequenza cumulata |
| Donna | 261 | 0.37 | 0.37 |
| Uomo | 453 | 0.63 | 1.00 |
N= Frequenza assoluta
Cosa sono le frequenze ?
Con un grafico comprendiamo ancora più facilmente il tutto!

Adesso sappiamo che sulla nave vi erano più uomini che donne.
A questo punto potremmo formulare delle ipotesi come:
Il genere può influire sulla sopravvivenza?
Prima di effettuare un modello possiamo osservare la sopravvivenza con una semplice statistica descrittiva bivariata al genere.
| Genere | Sopravvissuto | N | Frequenza | Frequenza cumulata |
| Donna | 0 | 64 | 0.25 | 0.25 |
| Donna | 1 | 197 | 0.75 | 1.00 |
| Uomo | 0 | 360 | 0.79 | 0.79 |
| Uomo | 1 | 93 | 0.21 | 1.00 |
0= non sopravvissuto
1= sopravvissuto
Comprendiamo meglio graficamente:

Sia dal grafico che dalla tabella comprendiamo come gli uomini siano sopravvissuti meno rispetto alle donne. Dalla tabella si evince che sono sopravvissute il 75% delle donne rispetto al numero totale delle donne, mentre solo il 21% degli uomini sono sopravvissuti rispetto al numero totale degli uomini.
In questo esempio sia la variabile genere (uomo/donna) sia la variabile sopravvissuto (sì/no) sono due variabili chiamate dummy (fattoriali con 2 modalità). La variabile genere, in questo caso, può avere solo due valori: uomo o donna, e la variabile sopravvissuto può avere solo due valori 0 (no), 1 (sì).
Esempio 2: Tariffa
La tariffa del biglietto è una variabile continua, perciò possiamo usare media, mediana, massimo, minimo, ecc…
| Minimo | 0.00 |
| Primo quartile | 7.91 |
| Media | 32.20 |
| Mediana | 14.45 |
| Terzo quartile | 31.00 |
| Massimo | 512.33 |
| Scarto quadratico medio | 49.69 |
Possiamo osservare ciò graficamente tramite un Box-plot:

Il seguente grafico ci informa che ci sono dei dati “strani” chiamati in gergo statistico outlier .
Il successivo grafico è senza outlier:

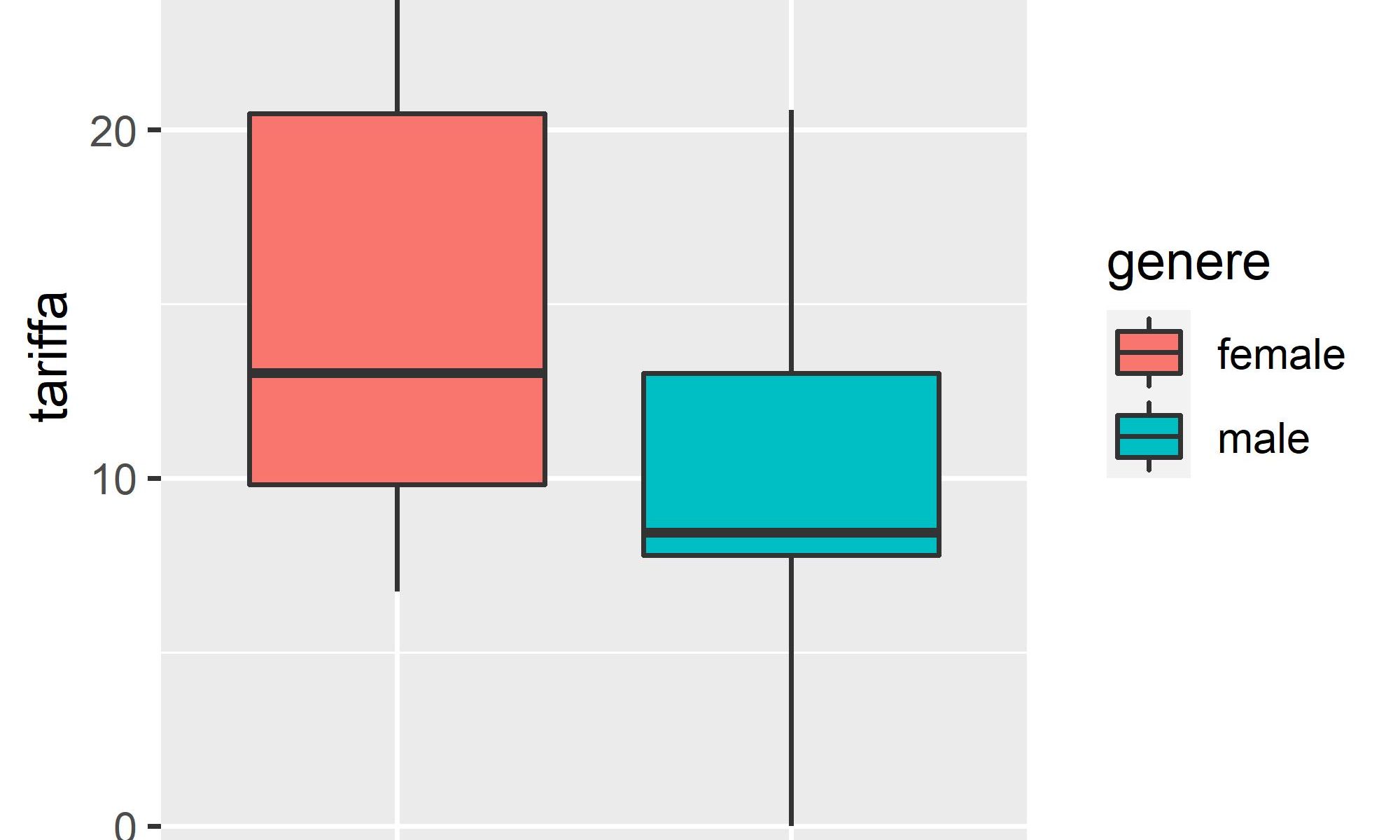
Potremmo chiederci se c’è una differenza nella tariffa basata sul genere

Sembrerebbe proprio di sì!
Potremmo formulare delle ipotesi sul perché vi siano tali differenze e poi verificarle.
Come abbiamo appena visto effettuando le statistiche descrittive su alcune variabili abbiamo potuto formulare delle semplici domande. Completando tutte le descrittive avremo tutti gli elementi per poter effettuare delle ipotesi che verranno confermate o rigettate con analisi successive (modelli, test, ecc…).